pliss pomozcie:( ULKA :(: Funkcje Jednym z miejsc zerowych f.kwadratowej jest liczba 1.Maksymalny przedzial w ktorym ta funkcja jest malejaca to <3,∞).Najwieksza wartosc funkcji f w przedziale <7,8> jest rowna −12.Wyznacz wzor funkcji f i narysuj jej wykres

ula:

	−b+√Δ
liczba 1 jest pierwiastkiem → 1=		Δ≥0
	2a

funkcja malejąca w przedziale <3;∞) → W(p,q) p=3 z tych dwuch wynika,że ramina są do dołu −12=a*7²+b*7+c zrób ztego układ równań i oblicz a,b,c

ULKA :(: p=3 a ile q= to ma byc uklad z trzema niewiadomymi/ o matko:(

ULKA :(: nikt mi nie pomoze:(

ULKA :(: −12=a*7²+b*7+c −12=a*8²+b*8+c 3= −b/2a taki ma byc uklad z trzema niewiadomymi/ niech ktos sprawdzi

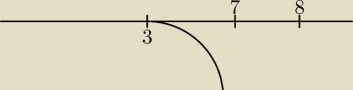
Godzio: może tak skoro mamy jedno miejsce zerow i wierzchołek: wierzchołek jest średnią arytmetyczną mz

	x1 + x2
p =
	2

6= 1 + x₂ 5=x₂ zobacz na skic: największa wartość w przedziale <7,8> jest − 12 jesli narysujemy sobie szkic to widzimy ze ta największa wartość jest dla f(7) = −12 i zapisujemy postać iloczynową i podstawiamy dany punkt: f(7) = −12 => A(7,−12) f(x) = a(x−x₁)(x−x₂) = a(x−1)(x−5) f(x) = a(x−1)(x−5) −12 = a(7−1)(7−5) −12 = a*6*2 a=−1 powracamy do naszej postaci f(x) = −(x−1)(x−5) = −(x² −6x +5) = −x²−6x+5

	−Δ		16
z wykresem sobie już poradzisz x1=1 x2 = 5 p=3 q=		=		= 4
	−4		4

Godzio: w twoim równaniu f(7) = −12 i f(8) = −12 więc pierwsze jest dobrze ale 2 już nie

Godzio: pomyłka f(x) = −(x²−6x+5) = −x² + 6x −5

ULKA :(: ogromne dzieki...ktos mnie w koncu wysluchal!